Original: Shotgun damage: New Model, posted July 14th, 2015
Author: leptis
THIS POST IS PREVIOUS TO FALL/2015 CHANGES: IT REMAINS VALID AS QUALITATIVE DESCRIPTION OF SHOTGUNS BEHAVIOUR. VALUES BELOW 24 METERS ARE VALID QUANTITATIVELY.
NEW POST:
In a previous post I have given some results of damage depending on the number of pellets cartridge based on a probabilistic approach which assumed uniform distribution in the circle of dispersion (if the head occupies 10% of the circle will receive 10% of the pellets).
Actually pellets are randomized to the radius and angle which gives a distribution with a bias to the center.
I have applied the MonteCarlo method which is a computational algorithm suitable for this type of phenomena, generating 136,080 pellets fired for each distance, and evaluating therefore 2.73 million pellets for each shotgun configuration (ads, choke, aiming…).
The MonteCarlo method basically consists of generating a large number of random events (with the rules of the physical process) to obtain a synthetic sample that can be analyzed statistically.
I used a simplified and targeted hitbox.
More details of methodology here:
Each pellet is generated within the circle of dispersion:
r = random (0,1) * R where R = D * TAN (ang) and ang = function (choke)
A = random (0,1) * 2 * PI
Here you see the dispersion (2.000 pellets)

Xd = COS (A) and Yd = SIN (A) are calculated
Pellets are “clusterized” in groups of 12, 15,18 and 21.
The spread Xs, Ys of center of the circle of dispersion are calculated in the same way (polar random too) depending on the form of targeted (ADS, HIP…) that applies equally to each group previously calculated.
If the point aimed is Xa, Ya final coordinates of the pellet are
X = Xa + Xs + Yd and Y = Ya + Ys + Yd
130,080 pellets are generated for each distance.
It is used this simplified Hitbox:
Head 0.20m (width) x 0.30 m (height), damage multiplier = 1
Chest 0.50m (width) x 0.30 m (height), damage multiplier = 1
Stomach 0.50 m (width) x 0.40 m (height), damage multiplier = 0.93
Legs 0.50 m (width) x 0.90 m (height), damage multiplier = 0.93
The origin X=0 and Y=0 is centered in chest.
Arms or defensive spec are not considered.
An algorithm for hit (in or out) is calculated for each pellet.
Damage for each group is obtained and the statistical parameters: mean, median, mode, standard deviation, quartiles, values> 100 and> 50, etc … are obtained for every 5 meters between 0 and 50 m and 10 m between 50 and 100 m.
Given the method used, the geometric irregularity of the hitbox and that the value of the damage is discreet (There is not half pellets) obtained curves are not smooth and have a tendency to step.
EXCEL was used.
To not write a long post I will display results with little comment, although each graph provide enough material for a long discussion.
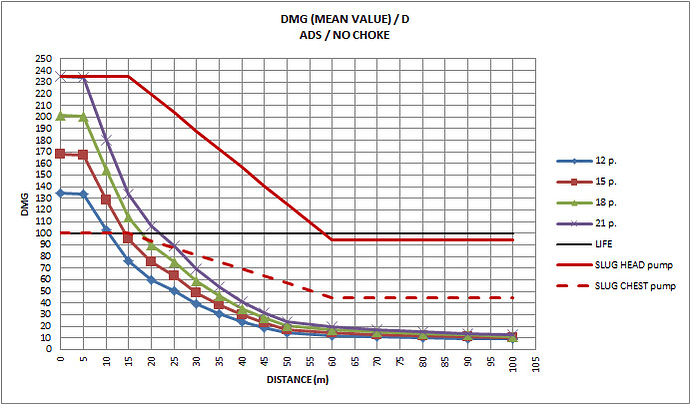
The results, for aiming to center of chest (Xa=0, Ya=0) and ADS, are:
Mean values of damage vs distance (slug damage for comparation):
Distances for mean value 100, 11 m for 12 p., 14 m for 15 p., 17 m for 18 p. and 22m for 21 p…
Probability of damage> 100 vs distance:
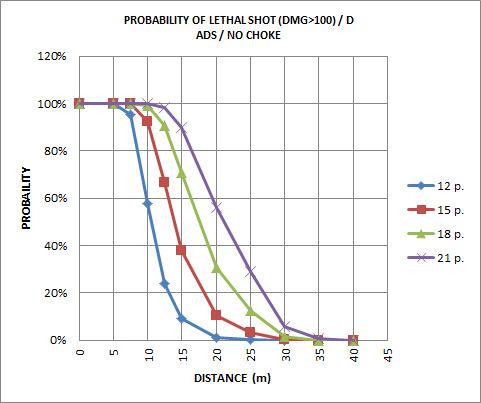
A shot with 21 pellets kill at 10 m with pprobability 100%, and has a wery small probabiliy to kill at 35 m.
Variation of the standard deviation of damage vs distance:
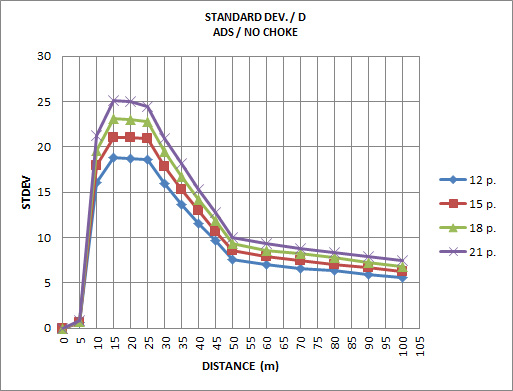
Standard deviation varies nonlinearly with maximum dispersion of damage at 20 m (approx).
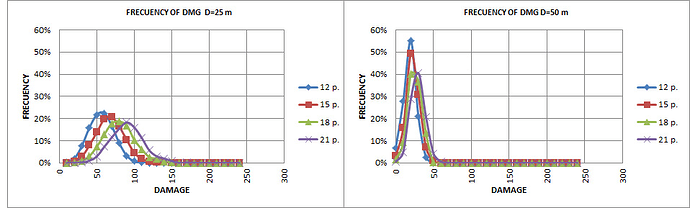
Frequency of damage at a specified distance (25 and 50 m calculated) (this is the lateral dispersion around mean value).
It can be assumed normal distributions of damage despite a small asymmetry (right tail).
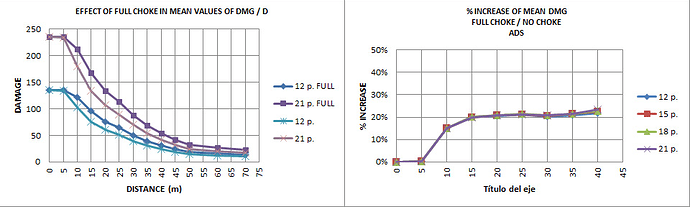
Full choke effect in the mean damage (only 12 p and 21 p are represented for better clarity) and % of increase of mean damage:
Full choke improves the mean damage 20% (approx.) and is not very useful at very short range. The effect is like moving curves damage to 5 m further (approx.).
Possibility of analytical modeling with logarithmic models (21 pellets):
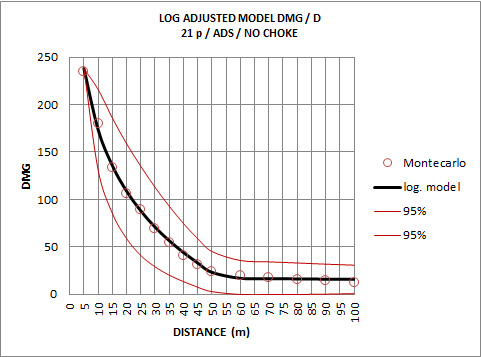
We can model curves of damage in three domains, constant maximum damage up to 5 m (exactly to 5.96 m) - not represented- and two logarithmic models, one from 5 to 50 and another from 50 meters.
The confidence interval of 95% is represented. Note the variation of size due to variation of standard deviation. No deviation exits at 5 m: all pellets in target.
A very approximate mean value of the damage can be obtained with the formula (discussion below):
DMG=9 x Np x DMGu(D) / D
Np = Number of pellets in the cartridge
DMGu = Unitary pellet damage at distance D, obtained from the basic curve damage.
D = Distance
Use:
Between 0 and 5 m maximum damage = NpxDMGu (0)
Between 15 and 100 = Formula
For 10 m, average value of 5 m to 15 m.
Here you can see the graphics ( 5 m and 10 m) that represent the area of aiming in which one death with 100% probability and 50% Probability is achieved. 12 -left- and 21 pellets -right-.